Signals are patterns of meaningful sound, noise, or pictorial representations of data.
Sound signals include speech, music, and noise.
Noise is any kind of disturbance that distorts a meaningful sound pattern.
Pictorial representations of data include text, images, and video.
Signal processing allows us to capture and manipulate signals within physical systems.
Electronic devices that process signals include computers, smartphones, televisions, satellites, radios, weather-forecasting systems, cameras, IoT devices, sensors, electronic instrumentation devices (such as ammeters and voltmeters), and medical equipment (such as BP monitors).
Engineering branches that deal with signal processing include electrical, electronics, instrumentation, computer science, and biomedical engineering.
Signals & Systems
The purpose of this guide is to help students learn about Signals and Systems.
Signals and Systems covers various topics such as:
- Continuous and Discrete Signals
- Linear Time-Invariant Systems
- Fourier Series
- Signal Properties
- Time and Frequency Domains
- Sampling Theorem
- Communication Systems
- The Laplace Transform
- The z-Transform
- Linear Feedback Systems
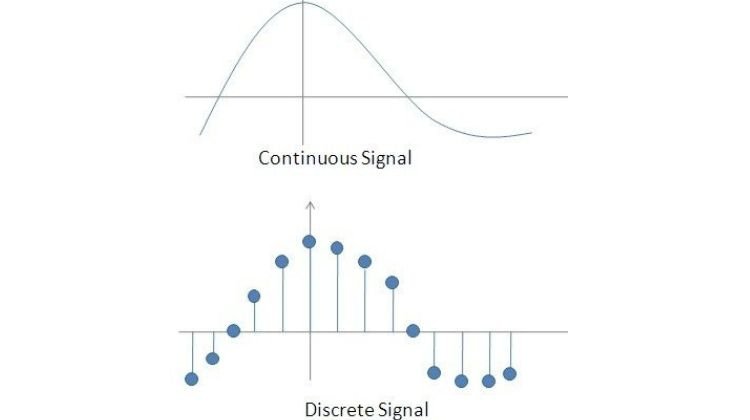
Continuous & Discrete Signals:
Continuous signals have a fixed pattern with respect to time such as voice and temperature.
Discrete signals vary over time such as demographics, stock market index.
Even & Odd Signals:
Even signal is symmetrical with the vertical axis like aeroplane flying with two wings.
Odd signal is anti-symmetrical with respect to time such as every person has a unique fingerprint.
Sinusoidal & Exponential Signals:
A sinusoidal signal has a fixed amplitude and frequency with respect to time, like a pendulum oscillating.
Exponential signals grow or decay over time, such as population growth or radioactive decay.
Unit Impulse & Unit Step Function:
A unit impulse is sampled data of a unit step function.
Unit impulse & unit step function can be continuous or discrete.
One second is a continuous unit impulse, and one hour is a continuous unit step in the time domain.
A discrete unit impulse can be denoted by a single function performed by a calculator (x + y = z), and a discrete unit step function by multiple calculations performed.
Linear Time Invariant System:
A linear time-invariant system sequence can be represented by the following equation: X(n) = x(1) + x(2) + x(3) + …
In a linear time-invariant system, the input signal changes with time but the output remains the same.
Take the example of the transformation in the mechanism used to send messages.
At the primary stage, we used postal mail, then phone calls or voice mail, and now we use the internet to send email, chat, and video call.
The sequence and process change with time but are connected, and the output remains the same.
Modern physical systems are built and upgraded for our convenience and better lifestyle.
Characteristics of Physical Systems:
A physical system can be described based on its characteristics and behaviour, such as input vs. output ratio, power consumption, life duration, and cost.
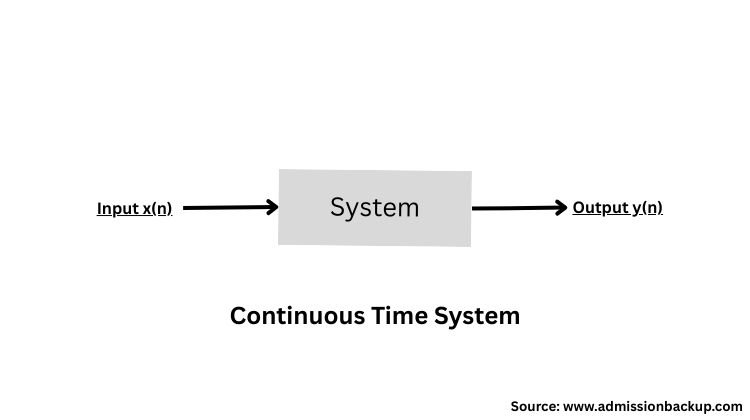
A continuous-time system can process a signal input to produce a single output, for example, a fan or a washing machine.
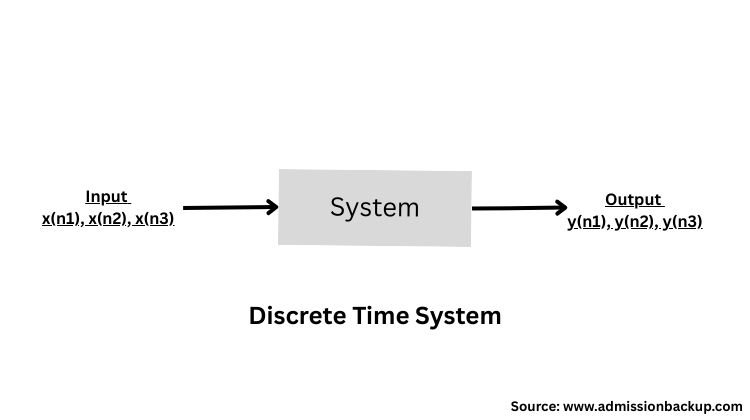
A discrete-time system can process multiple signals to produce multiple outputs, for example, a smartphone can perform various tasks such as calculation, messaging, phone calls, radio, camera functions, text editing, and internet access.
Fourier Series Analysis:
Fourier series analysis of continuous and discrete time systems represents that the output vs. input exponentially rises with respect to time.
This fundamental concept was developed by French mathematician and physicist Joseph Fourier and Leonhard Euler.
Properties of Signal:
Signals have different properties that can be utilised to make physical systems as per requirement and need.
Some of the properties of signals include amplitude, frequency, time reversal, linearity, time constant, period, time invariance, singularity, and duality.
Examples include audio and video streaming devices that can increase and decrease the volume, fast-forward, rewind, and change the playback speed.
Time and Frequency Characteristics of Signals & Systems:
In a 1st-order system, the magnitude in the frequency domain decreases with time due to the ripple effect and resistance in the traversing medium.
In a 2nd-order system, to increase the magnitude of the output power vs. the applied input, conductors were used (Satellite and Cable Television).
A more advanced transmission system is built using optical fibres for the transmission of data and messages across the globe, as light travels faster than sound.
The telephone was invented by Sir Alexander Graham Bell to transmit messages over long distances using cables and wires.
As air has resistance, charge cannot travel over long distances, as the magnitude of frequency is directly proportional to its amplitude.
Sampling Theorem:
Sampling of data at discrete time intervals for a period allows us to build cost-effective and time-efficient linear time-invariant systems.
It is a mathematical concept that allows us to filter data using electronic equipment and devices by converting analog signals to digital signals.
Communication Systems:
A digital communication system is a network used for radio broadcasting, satellite transmission, telecommunication, and providing internet access.
Frequency Bandwidth of Communication Channel:
- Audible Voice: 200 Hz – 4 kHz
- Radio Frequency: 500 kHz – 2 MHz
- Satellite Communication: 30 – 300 MHz
- Telecommunication: 6 – 30 GHz
- Optical Fiber: 10³ – 10⁷ GHz
A message signal is sent over a carrier signal using modulation techniques and is demodulated at the receiving end.
Multiple message signals can be sent over a wider channel using multiplexing and demultiplexing techniques.
The Laplace Transform:
The Laplace Transform is a mathematical analysis of linear time-invariant systems.
Any LTI system, to be stable and causal, must be bilateral.
H(s) = (1/s + 1)(1/s + 2) represents the Laplace Transform of a cascade of two first-order systems.
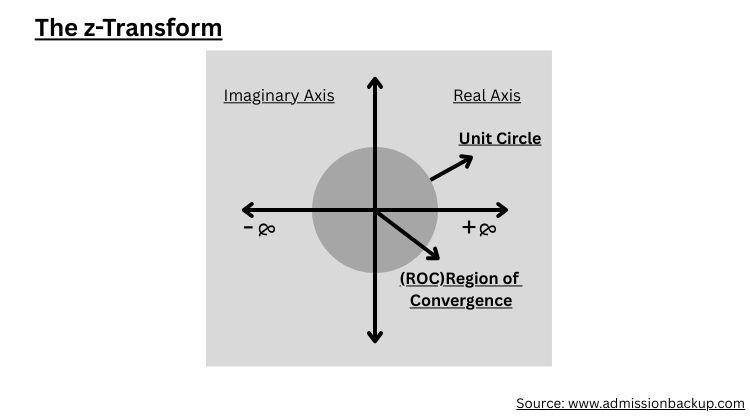
The z-Transform:
The z-Transform is a mathematical analysis of discrete-time LTI systems.
A discrete signal in the imaginary axis converges in the real axis only if it is rational and exponential.
x[n] = X(z) represents the z-Transform of a discrete-time signal, and x[-n] = X(1/z) represents the inverse z-Transform of a discrete-time signal.
Any discrete linear time-invariant system, to be stable and causal, must include the unit circle in the region of convergence (ROC).
Linear Feedback Systems:
A signal can be used to provide feedback to a system.
Such physical systems are called closed-loop systems or systems with a feedback loop.
Advantages of feedback loop systems include:
- Error control
- Performance improvement
- System stabilization
- Design of advanced systems
Conclusion:
Signals & Systems is a very important engineering discipline that develops the concepts and techniques for building modern electronic devices.
Signals have properties, as energy is the convolution of mass and light, and they propagate through a medium (air, water, or vacuum).
To learn more about Signals & Systems, interested students can join a B.Tech in Electrical Engineering or Electronics and Communication Engineering.
For career consultation, please contact our helpline at +91 8546881677.





